SmoothQuant尺度融合策略在高效Transformer量化中的应用

• 仓库README链接：README.md
• 本文件 md 源码链接：SmoothQuantInFlux.md

快速开始

算法实现与验证demo

代码详情参考 test_flux_double_anti.py

graph TD
    A[初始化FluxTransformerBlock_anti] --> B[加载原始模型参数]
    B --> C[生成Smooth Scale因子（固定种子）]
    
    C --> D1[QKV投影层融合]
    D1 --> D2[下调AdaLayerNorm参数]
    D2 --> D3[上调QKV投影层权重]
    
    C --> E1[MLP Up投影层融合]
    E1 --> E2[下调MLP相关的AdaLayerNorm参数]
    E2 --> E3[上调MLP Up投影层权重]
    
    C --> F1[Att-O融合]
    F1 --> F2[下调Value投影层参数]
    F2 --> F3[上调注意力输出层权重]
    
    D3 --> G[验证输出等价性]
    E3 --> G
    F3 --> G
    
    G --> H{输出误差<阈值?}
    H -->|是| I[测试通过]
    H -->|否| J[测试失败]
    
    style I fill:#9f9,stroke:#333,stroke-width:2px
    style J fill:#f66,stroke:#333,stroke-width:2px

验证指标：

$$\text{输出误差} \quad \delta_y = \max_{i} \left| y_i^{\text{(orig)}} - y_i^{\text{(fused)}} \right|$$

要求$\delta_y < 10^{-5}$以保证数值等价性。

运行验证代码：

• Install from pip+git

pip install git+https://github.com/hhqx/FLUX.1-dev.git

• [Optional] install from source

# git clone <This repo>
git clone git@github.com:hhqx/FLUX.1-dev.git

cd FLUX.1-dev
pip install -e .

# 运行验证代码
python -m tests.test_anti_smooth.test_flux_double_anti

验证结果示例：

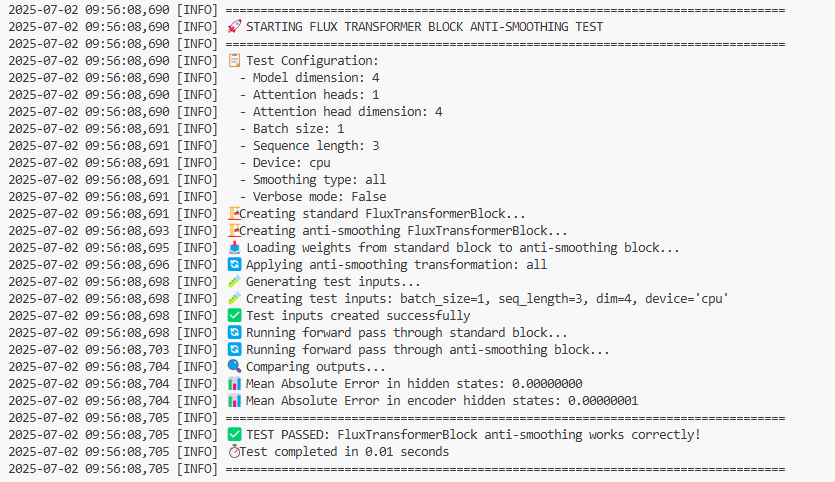
输出结果：

$ python -m tests.test_anti_smooth.test_flux_double_anti

第一章 绪论

1.1 研究背景
随着Transformer模型规模的不断扩大，模型量化成为降低计算资源需求的关键技术。然而，传统量化方法在非线性操作密集的Transformer架构中面临显著精度损失。SmoothQuant通过参数重校准技术，在维持计算等价性的前提下提升模型量化友好性，其核心在于尺度因子融合策略的创新设计。

graph LR
    subgraph "原始计算路径"
        A1[归一化层] --> B1[特征输出]
        B1 --> C1[线性投影层]
        C1 --> D1[输出]
    end
    
    subgraph "应用SmoothQuant后"
        A2[归一化层÷S] --> B2[缩小的特征输出]
        B2 --> C2[S×线性投影层]
        C2 --> D2[等价输出]
    end
    
    style D1 fill:#f9f,stroke:#333,stroke-width:2px
    style D2 fill:#f9f,stroke:#333,stroke-width:2px
    style B2 fill:#bbf,stroke:#333,stroke-width:1px
    style C2 fill:#bbf,stroke:#333,stroke-width:1px

1.2 研究内容
本章聚焦SmoothQuant在Transformer量化中的尺度融合机制，通过数学建模严格推导其在四类关键组件（QKV投影-归一化层、MLP上行投影-归一化层、MLP下行投影-上行投影层、注意力输出层-Value投影层）的等价性与非等价性条件，为高效量化提供理论基础。

第二章 SmoothQuant尺度融合在多模态AdaNorm中的设计与实现

2.1 QKV投影与AdaLayerNorm融合的等价性方案

建模过程：
设输入$\mathbf{x} \in \mathbb{R}^{d}$，AdaLayerNormZero输出：

$$\mathbf{h} = \underbrace{\text{norm}(\mathbf{x})}_{\text{归一化}} \odot \underbrace{(1 + \mathbf{g}_{\text{msa}})}_{\text{自适应缩放}} + \underbrace{\mathbf{s}_{\text{msa}}}_{\text{自适应平移}}$$

graph TD
    subgraph "AdaLayerNormZero Forward Computation"
        Emb[嵌入向量] --> SiLU[SiLU激活]
        SiLU --> Linear[线性变换]
        Linear --> Chunk["分块操作"]
        Chunk --> |shift_msa| ShiftPath["+"]
        Chunk --> |scale_msa| ScalePath["×"]
        Input[输入 x] --> Norm["norm(x)"]
        Norm --> ScalePath
        ScalePath --> |"X*(1+scale_msa)"| ShiftPath["add"]
        ShiftPath --> |"X*(1+scale_msa)+shift_msa"| Output["输出"]
    end

QKV投影输出：

$$\mathbf{y} = \mathbf{h} \mathbf{W}_{\text{qkv}}, \quad \mathbf{W}_{\text{qkv}} \in \mathbb{R}^{d \times 3d}$$

尺度融合变换：

1. 生成尺度因子：

   $$\boldsymbol{\sigma} = 2 + |\mathcal{N}(0, \mathbf{I})| \in \mathbb{R}^{d}$$

   （确定性生成）
2. 归一化层参数降尺度：

   $$\begin{aligned} \mathbf{W}_{\text{norm,shift}}' &= \mathbf{W}_{\text{norm,shift}} \cdot \text{diag}(\boldsymbol{\sigma})^{-1} \\ \mathbf{b}_{\text{norm,shift}}' &= \mathbf{b}_{\text{norm,shift}} \cdot \text{diag}(\boldsymbol{\sigma})^{-1} \\ \mathbf{W}_{\text{norm,scale}}' &= \mathbf{W}_{\text{norm,scale}} \cdot \text{diag}(\boldsymbol{\sigma})^{-1} \\ \mathbf{b}_{\text{norm,scale}}' &= (\mathbf{b}_{\text{norm,scale}} + \mathbf{1}) \cdot \text{diag}(\boldsymbol{\sigma})^{-1} - \mathbf{1} \end{aligned}$$

3. QKV投影升尺度：

   $$\mathbf{W}_{\text{qkv}}' = \text{diag}(\boldsymbol{\sigma}) \cdot \mathbf{W}_{\text{qkv}}$$

graph TD
    subgraph "QKV AdaNorm 异常值抑制"
        Ada["AdaLayerNormZero"] --> QKV["QKV Projection"]
        QKV --> Out["Output"]
        
        Smooth["Generate scale"] --> ScaleDown["AdaLayerNorm Parameter Downscaling"]
        Smooth --> ScaleUp["QKV Weight Upscaling"]
        
        ScaleDown -.-> |"W_norm · diag(σ)^-1"| Ada
        ScaleUp -.-> |"diag(σ) · W_qkv"| QKV
    end
    
    style ScaleDown fill:#bbf,stroke:#333,stroke-width:1px
    style ScaleUp fill:#bbf,stroke:#333,stroke-width:1px

此时：

$$(1 + \mathbf{g}_{\text{msa}}') = (1 + \mathbf{g}_{\text{msa}}) \text{diag}(\boldsymbol{\sigma})^{-1}$$

$$\mathbf{s}_{\text{msa}}' = \mathbf{s}_{\text{msa}} \cdot \text{diag}(\boldsymbol{\sigma})^{-1}$$

等价性证明：
原始输出：

$$\mathbf{y} = \mathbf{h} \mathbf{W}_{\text{qkv}} = \left[ \text{norm}(\mathbf{x}) \odot (1 + \mathbf{g}_{\text{msa}}) + \mathbf{s}_{\text{msa}} \right] \mathbf{W}_{\text{qkv}}$$

融合后输出：

$$\begin{aligned} \mathbf{y}' &= \left[ \text{norm}(\mathbf{x}) \odot (1 + \mathbf{g}_{\text{msa}}') + \mathbf{s}_{\text{msa}}' \right] \mathbf{W}_{\text{qkv}}' \\ &= \left[ \text{norm}(\mathbf{x}) \odot \left( (1 + \mathbf{g}_{\text{msa}}) \text{diag}(\boldsymbol{\sigma})^{-1} \right) + \mathbf{s}_{\text{msa}} \text{diag}(\boldsymbol{\sigma})^{-1} \right] \left( \text{diag}(\boldsymbol{\sigma}) \mathbf{W}_{\text{qkv}} \right) \\ &= \left( \mathbf{h} \cdot \text{diag}(\boldsymbol{\sigma})^{-1} \right) \left( \text{diag}(\boldsymbol{\sigma}) \mathbf{W}_{\text{qkv}} \right) \\ &= \mathbf{h} \cdot \underbrace{\text{diag}(\boldsymbol{\sigma})^{-1} \text{diag}(\boldsymbol{\sigma})}_{\mathbf{I}} \cdot \mathbf{W}_{\text{qkv}} \\ &= \mathbf{y} \end{aligned}$$

故

$$\mathbf{y}' \equiv \mathbf{y}$$

graph LR
    x["输入 x"] --> Norm["norm(x)"]
    Norm --> M1["× (1 + scale_msa)"]
    M1 --> Add1["Add"]
    shift["shift_msa"] --> Add1
    Add1 --> M2["@ W_qkv"]
    M2 --> Out1["原始输出"]
    
    x2["输入 x"] --> Norm2["norm(x)"]
    Norm2 --> M3["× (1 + scale_msa)/S"]
    M3 --> Add2["Add"]
    shift2["shift_msa/S"] --> Add2
    Add2 --> M4["@ (W_qkv·S)"]
    M4 --> Out2["融合后输出"]
    
    Out1 --> Equal["="]
    Out2 --> Equal
    
    style Equal fill:#9f9,stroke:#333,stroke-width:4px
    style M3 fill:#bbf,stroke:#333,stroke-width:1px
    style M4 fill:#bbf,stroke:#333,stroke-width:1px

2.2 MLP up投影层与AdaLayerNorm融合的等价性方案

建模过程：
设输入向量为 $\mathbf{x} \in \mathbb{R}^{1 \times d_{\text{in}}}$，上行投影权重矩阵为 $\mathbf{W}_{\text{up}} \in \mathbb{R}^{d_{\text{in}} \times d_{\text{hid}}}$，偏置向量为 $\mathbf{b}_{\text{up}} \in \mathbb{R}^{1 \times d_{\text{hid}}}$。

上行投影输出为：

$$\mathbf{u} = \mathbf{x} \mathbf{W}_{\text{up}} + \mathbf{b}_{\text{up}}$$

其中 $\mathbf{u} \in \mathbb{R}^{1 \times d_{\text{hid}}}$。

graph LR
    subgraph "原始MLP路径"
        AdaNorm1[AdaLayerNorm] --> |scale_mlp, shift_mlp| Norm1[归一化输出]
        Norm1 --> MLPUp1[MLP Up投影]
        MLPUp1 --> Out1[特征输出]
    end
    
    subgraph "融合后MLP路径"
        AdaNorm2[AdaLayerNorm] --> |scale_mlp÷S, shift_mlp÷S| Norm2[缩小的归一化输出]
        Norm2 --> MLPUp2[MLP Up投影×S]
        MLPUp2 --> Out2[等价特征输出]
    end
    
    style Out1 fill:#f96,stroke:#333,stroke-width:2px
    style Out2 fill:#f96,stroke:#333,stroke-width:2px
    style Norm2 fill:#bbf,stroke:#333,stroke-width:1px
    style MLPUp2 fill:#bbf,stroke:#333,stroke-width:1px

尺度融合变换：
定义对角尺度矩阵 $\mathbf{S} = \operatorname{diag}(\boldsymbol{\sigma}) \in \mathbb{R}^{d_{\text{hid}} \times d_{\text{hid}}}$，其中 $\boldsymbol{\sigma} = (\sigma_1, \sigma_2, \dots, \sigma_{d_{\text{hid}}})^\top > \mathbf{0}$。

MLP上行投影参数变换：

$$\mathbf{W}_{\text{up}}' = \text{diag}(\boldsymbol{\sigma}) \cdot \mathbf{W}_{\text{up}}, \quad \mathbf{s}_{\text{mlp}}' = \mathbf{s}_{\text{mlp}} \cdot \text{diag}(\boldsymbol{\sigma})^{-1}, \quad 1 + \mathbf{g}_{\text{mlp}}' = (1 + \mathbf{g}_{\text{mlp}}) \cdot \text{diag}(\boldsymbol{\sigma})^{-1}$$

融合后计算过程：

$$\begin{aligned} \mathbf{z}' &= [\text{norm}(\mathbf{x}) \odot (1 + \mathbf{g}'_{\text{mlp}}) + \mathbf{s}'_{\text{mlp}}] @ \mathbf{W}'_{\text{up}} \\ &= [\text{norm}(\mathbf{x}) \odot ((1 + \mathbf{g}_{\text{mlp}}) \cdot \text{diag}(\boldsymbol{\sigma})^{-1}) + \mathbf{s}_{\text{mlp}} \cdot \text{diag}(\boldsymbol{\sigma})^{-1}] @ (\text{diag}(\boldsymbol{\sigma}) \cdot \mathbf{W}_{\text{up}}) \\ &= [(\text{norm}(\mathbf{x}) \odot (1 + \mathbf{g}_{\text{mlp}}) + \mathbf{s}_{\text{mlp}}) \cdot \text{diag}(\boldsymbol{\sigma})^{-1}] @ (\text{diag}(\boldsymbol{\sigma}) \cdot \mathbf{W}_{\text{up}}) \\ &= (\mathbf{h} \cdot \text{diag}(\boldsymbol{\sigma})^{-1}) @ (\text{diag}(\boldsymbol{\sigma}) \cdot \mathbf{W}_{\text{up}}) \\ &= \mathbf{h} @ (\text{diag}(\boldsymbol{\sigma})^{-1} \cdot \text{diag}(\boldsymbol{\sigma})) @ \mathbf{W}_{\text{up}} \\ &= \mathbf{h} @ \mathbf{I} @ \mathbf{W}_{\text{up}} \\ &= \mathbf{h} @ \mathbf{W}_{\text{up}} \\ &= \mathbf{z} \end{aligned}$$

2.3 MLP下行投影融合的非等价性

建模过程：
设输入向量为 $\mathbf{x} \in \mathbb{R}^{1 \times d_{\text{in}}}$，上行投影权重矩阵为 $\mathbf{W}_{\text{up}} \in \mathbb{R}^{d_{\text{in}} \times d_{\text{hid}}}$，偏置向量为 $\mathbf{b}_{\text{up}} \in \mathbb{R}^{1 \times d_{\text{hid}}}$。

上行投影输出为：

$$\mathbf{u} = \mathbf{x} \mathbf{W}_{\text{up}} + \mathbf{b}_{\text{up}}$$

其中 $\mathbf{u} \in \mathbb{R}^{1 \times d_{\text{hid}}}$。

激活函数 $f: \mathbb{R} \to \mathbb{R}$ 逐元素作用于向量：

$$\mathbf{v} = f(\mathbf{u}) = \begin{bmatrix} f(u_1) & f(u_2) & \cdots & f(u_{d_{\text{hid}}}) \end{bmatrix}$$

下行投影权重矩阵为 $\mathbf{W}_{\text{down}} \in \mathbb{R}^{d_{\text{hid}} \times d_{\text{out}}}$，最终输出：

$$\mathbf{y} = \mathbf{v} \mathbf{W}_{\text{down}}$$

graph LR
    subgraph "原始前向路径"
        x1[输入] --> MLPUp1[MLP Up投影]
        MLPUp1 --> |线性输出| Act1["激活函数f()"]
        Act1 --> |非线性输出| MLPDown1[MLP Down投影]
        MLPDown1 --> Out1[输出]
    end
    
    subgraph "融合后路径（非等价）"
        x2[输入] --> MLPUp2["MLP Up投影÷S"]
        MLPUp2 --> |缩小的线性输出| Act2["激活函数f()"]
        Act2 --> |非线性修改后的输出| MLPDown2["S × MLP Down投影"]
        MLPDown2 --> Out2[不等价输出]
        
        NonEq["f(x/S) ≠ f(x)/S"]
    end
    
    style Out1 fill:#f96,stroke:#333,stroke-width:2px
    style Out2 fill:#f66,stroke:#333,stroke-width:2px,stroke-dasharray: 5 5
    style NonEq fill:#f66,stroke:#333,stroke-width:2px

尺度融合变换： 定义对角尺度矩阵 $\mathbf{S} = \operatorname{diag}(\boldsymbol{\sigma}) \in \mathbb{R}^{d_{\text{hid}} \times d_{\text{hid}}}$，其中 $\boldsymbol{\sigma} = (\sigma_1, \sigma_2, \dots, \sigma_{d_{\text{hid}}})^\top > \mathbf{0}$。

1. 上行投影参数变换：

   $$\mathbf{W}_{\text{up}}' = \mathbf{W}_{\text{up}} \mathbf{S}^{-1}, \quad \mathbf{b}_{\text{up}}' = \mathbf{b}_{\text{up}} \mathbf{S}^{-1}$$

   变换后上行投影输出：

   $$\mathbf{u}' = \mathbf{x} \mathbf{W}_{\text{up}}' + \mathbf{b}_{\text{up}}' = (\mathbf{x} \mathbf{W}_{\text{up}} + \mathbf{b}_{\text{up}}) \mathbf{S}^{-1} = \mathbf{u} \mathbf{S}^{-1}$$

2. 下行投影参数变换：

   $$\mathbf{W}_{\text{down}}' = \mathbf{S} \mathbf{W}_{\text{down}}$$

非等价性分析：
融合后输出：

$$\mathbf{y}' = f(\mathbf{u}') \mathbf{W}_{\text{down}}' = f(\mathbf{u} \mathbf{S}^{-1}) (\mathbf{S} \mathbf{W}_{\text{down}})$$

原始输出：

$$\mathbf{y} = f(\mathbf{u}) \mathbf{W}_{\text{down}}$$

等价性条件：
要使 $\mathbf{y}' = \mathbf{y}$，需满足：

$$f(\mathbf{u} \mathbf{S}^{-1}) \mathbf{S} = f(\mathbf{u})$$

即对每个分量 $j$： $f\left( \frac{u_j}{\sigma_j} \right) \sigma_j = f(u_j)$

对于非线性函数（如GELU或SiLU），这一等式不成立，即：

$$\text{activation}(\mathbf{u} \cdot \text{diag}(\boldsymbol{\sigma})^{-1}) \neq \text{activation}(\mathbf{u}) \cdot \text{diag}(\boldsymbol{\sigma})^{-1}$$

2.4 注意力输出层融合的等价性方案

建模过程：
Value投影输出：

$$\mathbf{V} = \mathbf{X} \mathbf{W}_v + \mathbf{b}_v$$

注意力权重：

$$\mathbf{A} = \text{softmax}\left( \frac{\mathbf{Q}\mathbf{K}^\top}{\sqrt{d}} \right)$$

输出投影：

$$\mathbf{y} = (\mathbf{A} \mathbf{V}) \mathbf{W}_o$$

graph TD
    subgraph "原始注意力计算"
        x1[输入] --> V1["Value投影 (x @ W_v + b_v)"]
        QK1["Q·K^T/√d"] --> Soft1["Softmax"]
        Soft1 --> Dot1["矩阵乘法"]
        V1 --> Dot1
        Dot1 --> AttO1["注意力输出投影"]
        AttO1 --> Out1[输出]
    end
    
    subgraph "融合后注意力计算"
        x2[输入] --> V2["Value投影 (x @ W_v/S + b_v/S)"]
        QK2["Q·K^T/√d"] --> Soft2["Softmax"]
        Soft2 --> Dot2["矩阵乘法"]
        V2 --> Dot2
        Dot2 --> AttO2["S × 注意力输出投影"]
        AttO2 --> Out2[等价输出]
    end
    
    style Out1 fill:#f96,stroke:#333,stroke-width:2px
    style Out2 fill:#f96,stroke:#333,stroke-width:2px
    style V2 fill:#bbf,stroke:#333,stroke-width:1px
    style AttO2 fill:#bbf,stroke:#333,stroke-width:1px

尺度融合变换：

1. Value投影降尺度：

   $$\mathbf{W}_v' = \mathbf{W}_v \text{diag}(\boldsymbol{\sigma})^{-1}, \quad \mathbf{b}_v' = \mathbf{b}_v \cdot \text{diag}(\boldsymbol{\sigma})^{-1}$$

2. 输出投影升尺度：

   $$\mathbf{W}_o' =\text{diag}(\boldsymbol{\sigma}) \mathbf{W}_o$$

等价性证明：
融合后计算路径：

$$\begin{aligned} \mathbf{V}' &= \mathbf{V} \text{diag}(\boldsymbol{\sigma})^{-1} \\ \mathbf{O}' &= \mathbf{A} \mathbf{V}' \\ &= \mathbf{A} \mathbf{V} \text{diag}(\boldsymbol{\sigma})^{-1} \\ &= \mathbf{O} \text{diag}(\boldsymbol{\sigma})^{-1} \\ \mathbf{y}' &= \mathbf{O}' \mathbf{W}_o' \\ &= \left( \mathbf{O} \text{diag}(\boldsymbol{\sigma})^{-1} \right) \left( \text{diag}(\boldsymbol{\sigma} \mathbf{W}_o ) \right) \\ &= \mathbf{O} \underbrace{\text{diag}(\boldsymbol{\sigma})^{-1} \text{diag}(\boldsymbol{\sigma})}_{\mathbf{I}} \mathbf{W}_o\\ &= \mathbf{y} \end{aligned}$$

线性矩阵乘法保持运算等价性。

graph TD
    subgraph "融合前注意力计算"
        V1["V = x @ W_v + b_v"] --> Att1["Attention计算"]
        Att1 --> O1["O = Softmax(QK^T/√d)·V"]
        O1 --> OutProj1["output = O @ W_o"]
    end
    
    subgraph "融合后注意力输出计算"
        V2["V' = x @ (W_v/S) + b_v/S = V/S"] --> Att2["Attention计算"]
        Att2 --> O2["O' = Softmax(QK^T/√d)·V' = O/S"]
        O2 --> OutProj2["output' = O' @ (W_o·S) = O @ W_o"]
    end
    
    OutProj1 --> Equal["="]
    OutProj2 --> Equal
    
    style Equal fill:#9f9,stroke:#333,stroke-width:4px
    style V2 fill:#bbf,stroke:#333,stroke-width:1px
    style O2 fill:#bbf,stroke:#333,stroke-width:1px
    style OutProj2 fill:#bbf,stroke:#333,stroke-width:1px

第四章 结论与讨论

1. 理论贡献：

   • 严格证明SmoothQuant在线性投影-归一化层组合中的计算等价性
   • 揭示非线性激活函数是破坏MLP下行投影等价性的根本原因
   • 建立注意力机制中跨层尺度融合的可行性条件

2. 工程指导：

   组件类型	可融合性	关键约束
   QKV投影+归一化	✓	尺度因子同步更新
   MLP上行+归一化	✓	偏置项特殊处理
   MLP下行+上行	✗	非线性激活不可逆
   注意力输出+Value	✓	矩阵乘法线性性

AdaNorm 融合前后权重参数对照表

表示约定说明：

1. 数学表示（列优先存储）：

   • 线性层运算：$\mathbf{Y} = \mathbf{X}W_{norm, scale} + \mathbf{b}$
   • 权重维度：$W_{norm, scale} \in \mathbb{R}^{\ast \times D}$

2. 代码实现（行优先存储）：

   • 线性层运算：$\mathbf{Y} = \mathbf{X}W_{norm, scale}^\top + \mathbf{b}$
   • 权重维度：$W_{norm,scale} \in \mathbb{R}^{D \times \ast}$

3. 操作符说明：

   • $D$：表示异常值抑制的维度，即AdaNorm的输出维度，与QKV投影层输入维度一致
   • $\boldsymbol{\sigma}$：尺度因子向量，通过 $\text{diag}(\boldsymbol{\sigma})$ 构造对角矩阵
   • $\otimes$：表示矩阵乘法 $\text{diag}(\boldsymbol{\sigma}) \cdot W$（维度适配广播）
   • $\frac{\square}{\boldsymbol{\sigma}}$：表示逐元素除以尺度因子

附录：数学符号表

安装与运行

安装方法

提供两种安装方式：

1. 从源代码安装 (推荐用于开发)

# 克隆项目仓库
git clone git@github.com:hhqx/FLUX.1-dev.git

# 进入项目目录
cd FLUX.1-dev

# 以开发模式安装
pip install -e .

2. 直接从GitHub安装 (适用于快速试用)

pip install git+https://github.com/hhqx/FLUX.1-dev.git

运行测试

执行验证测试脚本：

# 基础运行
python -m tests.test_anti_smooth.test_flux_double_anti

# 详细模式运行（显示完整日志）
python -m tests.test_anti_smooth.test_flux_double_anti --verbose

更多运行选项请参考：

python -m tests.test_anti_smooth.test_flux_double_anti --help